"Вертикальное" мышление

      Для решения этой задачи (задачи построения идеального пространства и идеальной системы) нам придётся прибегнуть к приёму, который используется, например, в молекулярной физике, где рассматривается такое понятие, как “идеальный газ”. Этот приём – идеализация реальных объектов (и процессов) оказался очень плодотворным, с его помощью стало возможным легко и наглядно описывать свойства газов. То же самое нам придётся проделать в отношении таких объектов, как пространство и система.
      Понятие пространства является одним из самых глубоких в философии и познании. Существуют разные взгляды на природу пространства. В одном случае пространство рассматривается как некое вместилище, ёмкость, в другом – как некая структура (реляционная и субстанциональная концепции пространства и времени). СФКМ исходит из предположения о существовании структуры у физического вакуума, поэтому здесь пространство – это структура, которая является одновременно и местом, где зарождаются и развиваются различные явления (которые мы воспринимаем как тела и процессы) и источником энергии для них и организующим фактором их формы. Но любой объект действительности обладает тем или иным набором свойств, признаков и даже у элементарных частиц этот набор не маленький. При построении идеального пространства используются лишь самые общие из них. Каковы эти свойства и признаки? Приведём цитату.
      "В своей деятельности мы обнаруживаем такие особенности структурной организации мира, что части и элементы, из которых построены материальные объекты, определённым образом расположены друг относительно друга, образуют некоторые устойчивые конфигурации, что задаёт границы объекта по отношению к окружающей среде. Можно сказать, что каждый объект характеризуется своеобразной "упаковкой" входящих в него элементов, их расположенностью относительно друг друга, и это делает любые объекты протяженными. Кроме того, каждый объект занимает какое-то место среди других объектов, граничит с ними.
      Все эти предельно общие свойства, выражающие структурную организацию материального мира, - свойства объектов быть протяженными, занимать место среди других, граничить с другими объектами – выступают как первые, наиболее общие характеристики пространства. Если их абстрагировать из действительности, отделить от самих материальных объектов, то мы получим представление о пространстве, как таковом".
      Из сказанного вытекает, что пространство можно "обнаружить" лишь через структуру объекта, помещённого в это пространство. Если из пространства "вынуть" объект с его структурой, то останутся места, которые занимали элементы и связи данной системы и к которым так же применимы предельно общие характеристики – протяженность, место, отграниченность.
      Все эти места и потенциальные связи между ними, которые занимали компоненты реальной системы, тоже можно рассматривать как элементы некой виртуальной системы, описываемые с помощью наиболее общих понятий – места и отношения.
      Таким образом, пространство как таковое можно рассматривать как некую структурированную совокупность "мест" и отношений между ними. Каждое такое место уникально, и ему можно присвоить индекс (имя), а связи (отношения), обозначить парами таких индексов.
      В пространстве, описываемом евклидовой геометрией, роль таких индексов играют наборы чисел – координат в выбранной системе отсчёта. Но поскольку пространство изначально представляет собой систему (и, возможно, не только виртуальную), то возможна и принципиально иная индексация содержащихся в нём мест – системная. Она-то и является естественной, в отличие от евклидовой, которую в этом контексте можно назвать условной. Такое пространство можно определить как системное.
      Но из этого следует, что и реальную систему, если абстрагироваться от всех её конкретных свойств, можно описать таким же способом. Такую систему можно определить как идеальную, а пространство, которое она занимает, как системное пространство. Таким образом, системное пространство – это отношения между элементами системы, выраженные через наиболее общие характеристики пространства (протяженность, место, отграниченность).

СИСТЕМНОЕ ПРОСТРАНСТВО ИДЕАЛЬНОЙ СИСТЕМЫ

      Последовательность наших рассуждений в процессе построения этой модели будет следующей.
      Если рассматривать ту или иную систему, абстрагируясь от её структуры, мы получим условно-атомарный, условно-бесструктурный объект, точку. Изобразим его, нарисовав замкнутый контур и отграниченную им часть поверхности закрасив (рисунок 14).

Рисунок 14

      Но из принципа системной организации действительности следует, что любой объект должен иметь структуру, т. е. состоять из каких-то частей, связанных между собой. В то же время он должен быть частью какой-то большей системы, включающей этот объект в качестве подсистемы (назовём её гиперсистемой, рисунок 15).

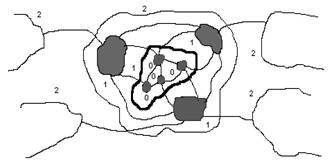
Рисунок 15

      Как мы можем видеть, на этих рисунках чередуются в определённом порядке всего два элемента: граница и пересекающая её связь. Какую роль здесь играет граница? Это поверхность какого-то реального физического тела, замыкающая в себе элементы этой системы, или нечто иное? Этот вопрос порождает другой, более интересный: а что вообще есть граница между телом и средой (при условии неограниченного действия принципа структурности материи)? Это вопрос философского ранга и ответ на него не столь прост, каким кажется поначалу. Чтобы не пускаться в обширные рассуждения, определим эту границу как условность, приём, позволяющий выделить уровни организации системы. Физический смысл этой границы (псевдограницы) – скачок свойств между системой и окружением.
      Снова обратимся к рисунку 15. На нём мы увидим три типа границ, позволяющих увидеть три уровня иерархии рассматриваемой системы. Четыре из них ограничивают небольшие заштрихованные области, обозначим их как границы 0-го уровня. У этих четырёх объектов есть одна общая граница (точнее – псевдограница); обозначим её (и ещё три таких же) как границы 1-го уровня. Которые ограничивают объекты 1-го уровня. В свою очередь, эти четыре объекта составляют объект 2-го уровня (соответственно ограниченный границей 2-го уровня) и т. д. Этот процесс можно продолжать долго (но применительно к реальной действительности вряд ли кто-то сможет сказать, насколько долго). Ясно лишь, что самая общая граница всегда совпадает с актуальной границей нашего познания.
      Но можно двигаться и в противоположном направлении. Объекты 0-го уровня – это тоже системы, которые, в свою очередь, состоят из каких-то объектов, каждый из которых имеет псевдограницу -1-го уровня, каждый из объектов -1-го уровня состоит из объектов -2-го уровня и так далее.

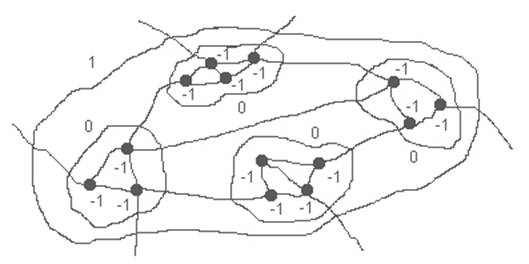
Рисунок 16

      Таким образом, мы видим, что актуальной становится проблема точки отсчёта для данного метода описания структуры системы. Можно ли, например, выбрать её так, чтобы избавиться от отрицательных индексов? Будем рассуждать так.
       На любую систему Σ можно смотреть двояко: "извне", как на некую бесструктурную целостность, как на атомарный объект, атомарный элемент какой-то другой системы (гиперсистемы), и "изнутри", когда возникает необходимость рассмотреть внутреннее устройство системы, её структуру. В этом случае нам придётся выделить следующие уровни организации системы Σ:
       0-й уровень, когда система Σ рассматривается как атомарный элемент гиперсистемы:

Рисунок 17

      1-й уровень, который содержит основные векторы структуры системы:

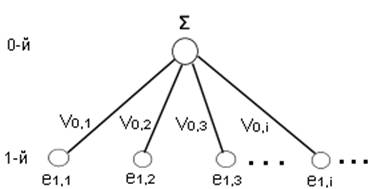
Рисунок 18

      Каждый элемент 1-го уровня также имеет структуру, которую можно представить в виде "дерева":

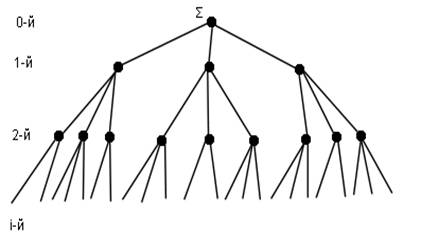
Рисунок 19

      И так вплоть до уровня, который мы выбрали, как атомарный (α – уровень):

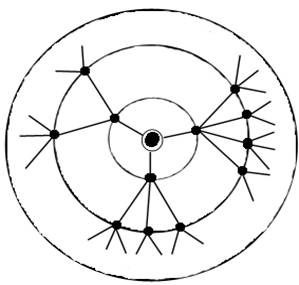
Рисунок 20

      Та же иерархия, но в концентрической форме.
      Но что же, всё-таки, есть система? Границы тела мы отвергли, определив их как псевдосущности. Остаются только связи! Да, есть ещё уровень атомов, но это тоже условность, эти объекты имеют структуру, мы просто условились её не рассматривать. Но это подразумевает, что наши "атомы" тоже сплошь состоят из связей, до какой бы степени "дробления" мы не дошли. Но тогда в нашей системе, кроме связей, ничего и не остаётся! Так ли это? Попробуем ответить на этот вопрос немного позже, тогда, когда хотя бы немного определимся с тем, что есть связи.
       Любая связь имеет две, скажем так, ипостаси. Одна из этих ипостасей – физический канал, другая – это то, что по нему движется (назовём его потоком ресурса). Каков характер взаимодействия между этими двумя сущностями – потоком ресурса и каналом? Здесь реализуется взаимодействие того рода, что канал определяет характер ресурса и параметры потока ресурса. Тем самым, он выступает в роли фактора, формирующего процесс движения потока ресурса и по этой причине может рассматриваться как управленческий фактор, как алгоритм. Таким образом, в явлении связи реализуется взаимодействие изменяемой (движение потока ресурса) и изменяющей (канала) сущностей, т. е. преобразование. В простейшем случае его можно определить, как транспортное.
      Что можно сказать о потоке ресурса? Поток в общем случае – это направленное движение каких-то объектов, частиц. Если использовать понятия протяженности и сечения, то поток – это сонаправленное движение совокупности каких-то объектов, протяженность которой (размер в направлении движения) больше, чем сечение (размер в направлении, перпендикулярном движению). Из принятого определения потока также следует, что он имеет дискретную структуру. Эта структура может быть как очень простой (скажем, перемещение таких систем-атомов, как жидкости, газы, сыпучие материалы), так и очень сложной (объектами потока могут также быть различные физические, химические, технические системы).
      Скажем, аналоговый сигнал в линии связи может иметь очень сложную структуру. Более того, в процессе преобразования любой объект (не только потоки "атомарного" вещества или энергии, но и "твёрдые" системы) можно рассматривать как поток ресурса, так как каждую такую систему необходимо сначала доставить к узлам разборки (операция диссоциации), или же совокупность компонентов доставить к узлам сборки системы (операция ассоциации).

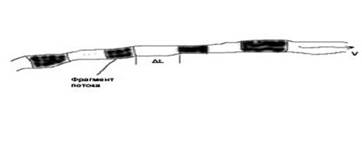
Рисунок 21

      Ещё о потоке ресурса можно сказать, что он движется с какой-то скоростью (которая может изменяться), а отдельные фрагменты потока как-то взаимодействуют между собой, (существует какое-то расстояние между ними) и с поверхностью канала. Потоки ресурса можно также классифицировать соответственно их природе (вещественные, энергетические, информационные и т. д.). Канал можно охарактеризовать по материалу, конфигурации (сечение, длина, топология), оптимальному значению нагрузки.
      Ещё одна важная характеристика потока – интенсивность (мощность). Это количество ресурса, который проходит через сечение канала за единицу времени. Зависит от скорости потока и наполнения канала (при выбранном сечении).
      Какие преобразования возможны над потоком ресурса? Все изменения в Природе, какими бы многообразными они ни казались, сводятся всего к трём типам: диссоциации (разборке), транспортировке (перемещению), и ассоциации (сборке). Изобразим это следующим образом.

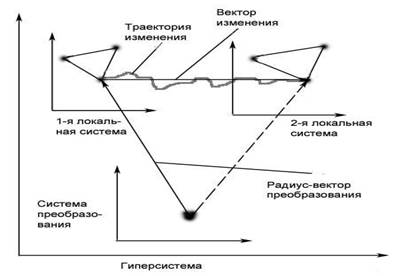
Рисунок 22

      Напомним, что мы рассматриваем преобразование на структурном пространстве. Введём некоторые соглашения относительно системных терминов. Любую систему можно изобразить с помощью точек и линий. И то, и другое – суть элементы системы. Но элементы-точки мы будем называть узлами, а элементы-линии – связями. Что такое – узлы, и какие действия можно выполнять над узлами системы?
      Любой узел – это система, он всегда является подсистемой какой-то более сложной системы. Если только он не объявлен атомом, над ним можно производить основные действия. Скажем, узел можно демонтировать, дезинтегрировать, разобрать полностью или частично, отключить от связей. Или наоборот, осуществить сборку (интеграцию) узла или его модификацию, подключить к связям. Ясно, что отключённый от связей узел можно транспортировать в другую систему и подключить его там.
      В составе преобразующей системы (а любая система в том или ином смысле преобразователь) узел играет роль системоформирующего фактора в отношении потока ресурса, проходящего через связи системы, с функциями интеграции-дезинтеграции или изменения энергетического состояния элементов потока (нагрева их или охлаждения). Узел осуществляет взаимодействие потоков, а, следовательно, их взаимное преобразование. В этом смысле весь наш мир можно рассматривать как одну всеобъемлющую преобразующую (и преобразующуюся) систему, как единый процесс преобразования.
      Что можно в этом контексте сказать о связях? Связь – это тоже элемент системы, который имеет свою структуру, он состоит из множества однородных элементов расположенных таким образом, чтобы была возможной транспортировка потока ресурса (или воздействия) от одного узла к другому. Над связями, как элементами системы, можно выполнять те же действия, что и над узлами.
       Если учесть вывод, к которому мы пришли ранее (что в системе, по сути, нет ничего, кроме каналов и потоков по ним), то получится, что манипуляции над узлами одновременно являются и манипуляциями над связями (а любой поток ресурса – это элементы каких-то узлов в стадии преобразования, в состоянии транспортировки). Основные характерные действия над связями – это блокировка, деблокировка и перекоммутация каналов. Но возможны и другие действия, как над каналами, так и над потоками ресурса. Можно менять характеристики канала – сечение, длину, топологию. Поток ресурса можно замедлить или ускорить, можно увеличить или уменьшить его интенсивность.
      Так что же являет собой собственно система? Вопрос этот весьма ёмкий и здесь дать полный ответ на него у нас не получится. Но кое-что сказать всё же необходимо.
      Система – это рельеф, образованный каналами, матрица-алгоритм, который обеспечивает протекание потоков ресурса и формирует их взаимодействие и преобразование, или это поток ресурса? Вопрос этот более сложный, чем может показаться на первый взгляд, а ответ на него следующий: система – это и то, и другое, потому что как каналы влияют на поведение потока ресурса, так и поток ресурса формирует рельеф, и это есть одно из проявлений развития. Ведь действительно, свойства стали, в каком-то смысле, формируют структуру сталеплавильной печи и металлообрабатывающего станка, а свойства нефти – структуру нефтеперерабатывающего завода. Да, не непосредственно, а через преобразователь – мышление человека (хотя можно утверждать, что само мышление человека сформировано подобным образом). Но в рамках процесса деятельности с целеполаганием, который осуществляет человек и для которого создаёт предметы-посредники и процессы посредники, мы договоримся считать систему каналов, рельеф, на котором происходит преобразование ресурса, транспортное и структурное, изменяющей сущностью, преобразователем, алгоритмом, а поток ресурса – изменяемой сущностью.

ПОРТРЕТ ИДЕАЛЬНОЙ СИСТЕМЫ

      Теперь, наконец, попробуем изобразить идеальную систему. Начнём с того, что изобразим несвязанное множество объектов. Договоримся, что это атомы будущей системы, т. е. внутренняя структура этих объектов нами рассматриваться не будет.

Рисунок 23

      А потом соединим эти атомы связями. Мы получим атомарный уровень системы.

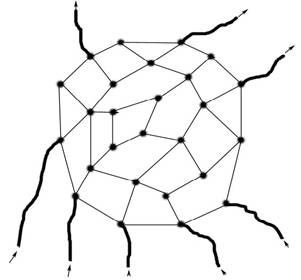
Рисунок 24

      Но любая система организована иерархически, и в ней можно выделить уровни организации. Покажем наглядно эту организацию, а для лучшего восприятия обозначим псевдограницы подсистем разными цветами.

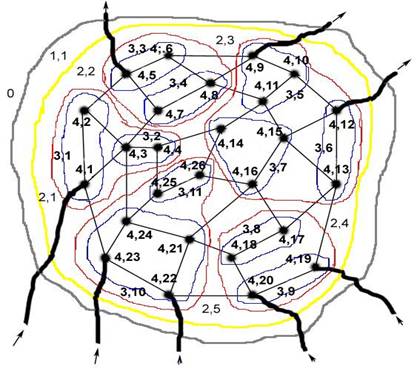
Рисунок 25

       0 - это псевдограница гиперсистемы Σ0; 1,1 - соответствует Σ1 (предполагается, что на этом уровне есть ещё 1,2 (Σ2), 1,3 (Σ3) и так далее…). В структуру системы 1,1 (или просто 1) входят пять подсистем: 2,1; 2,2; 2,3; 2,4; 2,5. В структуру подсистемы 2,1 входят её подсистемы 3,1 и 3,2. В структуру подсистемы 2,2 входят её подсистемы 3,3 и 3,4 (и так далее для всех подсистем 3-го уровня). В структуру подсистемы 3,1 входят атомарные элементы 4,1 и 4,2. В структуру подсистемы 3,2 входят атомарные элементы 4,3 и 4,4. (Остальные структурные элементы системы индексируются по аналогии).
       Таким образом, на 1-м уровне мы помещаем всегда один объект – систему, структуру которой рассматриваем. Как видим, чтобы обозначить элемент уровня, ему достаточно сопоставить две цифры: первая будет обозначать уровень организации системы, вторая – номер узла на этом уровне. Но вот чтобы зафиксировать координаты узла или связи в системе, двух цифр недостаточно.
       Наш рисунок (или аналогичный ему) можно сделать более наглядным, если представить структуру системы в форме концентрической диаграммы.

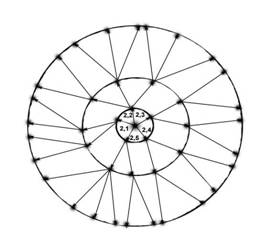
Рисунок 26

      Эта диаграмма отражает структуру системы, изображённой на предыдущем рисунке. Разберёмся, как ею пользоваться.
       Концентрические окружности, включая центральный объект, означают уровни организации системы. Отсчёт ведётся от центрального объекта, который символизирует систему в целом – это 1-й уровень. Следующие по порядку окружности символизируют соответственно 2-й, 3-й и 4-й уровни системы. Каждая точка символизирует узел – место пересечения каналов и взаимодействия потоков ресурсов. Каждая линия – группу связей, или вектор. Узел и вектор і–го уровня может распадаться на группу узлов и векторов і+1-го уровня. Но нам придётся немного модифицировать систему обозначений.
       На предыдущей схеме для обозначения каждого узла мы использовали две цифры. Первая из них указывала на уровень организации системы, к которому относится узел; вторая – "сквозной" номер объекта на этом уровне. Уровень организации (концентрическая окружность) здесь символизирует псевдограницу всех систем этого уровня, которые на этом уровне рассматриваются как атомарные.
       Узлы і-го уровня нумеруются последовательно, от 1 до n, где n - число всех узлов і-уровня. Каждый узел і-1-го уровня может распадаться на несколько узлов і-го уровня, а каждый узел і-го уровня - на несколько узлов і+1-го уровня. Это означает, что какой-то группе узлов і-го уровня можно поставить в соответствие число - номер узла і-1-го уровня, а какой-то группе узлов і+1-го уровня можно поставить в соответствие номер узла. И наоборот, каждому узлу і-1-го уровня можно поставить в соответствие два числа, ограничивающие диапазон номеров узлов і-го уровня, а каждому узлу і-го уровня - диапазон номеров узлов і+1-го уровня, также заданный двумя числами. Таким образом, получается, что структурные координаты любого узла системы системы любой сложности всегда содержат 5 (пять) чисел.

• Z - зона, уровень организации системы или номер псевдограницы;
• E - узел, элемент і-го уровня;
• G - группа (сектор) і-го уровня или элемент і-1-го уровня;
Диапазон номеров узлов і+1-го уровня, принадлежащих E - узлу і-го уровня;
• L - левая граница диапазона;
• R - правая граница диапазона.

       Таким образом, каждый узел любой системы можно описать при помощи пяти чисел, которые будут составлять его уникальное имя. Иначе - уникальное имя любого узла любой системы есть функция пяти координат.

U=U(Z,E,G,L,R).

       Изобразим структуру нашей системы ещё одним способом – в форме дерева. Так нам будет легче продемонстрировать предложенную методику обозначений.

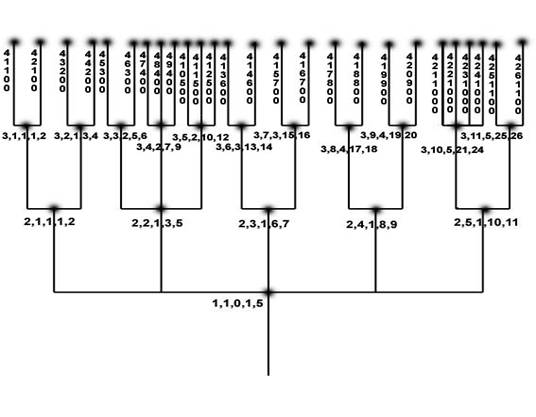
Рисунок 27

       Структуру системы можно ещё описать при помощи числового ряда следующим образом. Поставим возле каждого вектора i - го уровня число, которое будет означать число векторов i+1 - го уровня, на которые он распадается. Запишем ряд:

1, 5, 2, 3, 2, 2, 2, 2, 2, 2, 3, 3, 2, 2, 2, 2, 4, 2;

       Какая информация здесь содержится? Во-первых, этот ряд всегда начинается с числа 1, что означает, что вектор уровня 0,1 распадается на пять векторов уровня 1,2, а следующая за пятёркой группа из пяти чисел покажет, на сколько векторов уровня 2,3 распадётся каждый из пяти векторов уровня 1,2. Первое в этой пятёрке число 2. Это означает, что следующая сразу за группой из пяти чисел пара чисел 2,2 показывает, на сколько векторов уровня 3,4 распадётся каждый из первых двух векторов уровня 2,3 (на 2 и 2). Следующее в этой группе из пяти чисел число 3 означает, что следующая сразу за пятёркой чисел + парой 2,2 показывает, на сколько векторов уровня 3,4 распадётся каждый из следующих трёх векторов уровня 2,3 (на 2, 3 и 3) и т. д. Эта форма нам необходима будет для создания числового паспорта системы.
       Как уже упоминалось выше, вторым основным элементом системы (кроме узла) является связь. Связь это канал (или сумма каналов), по которым могут перемещаться потоки ресурса. Поскольку конкретный поток ресурса имеет направление, его ещё можно определить как вектор. Связь, которая объединяет несколько каналов, будем называть интегральной связью.
       Псевдограницу той или иной подсистемы пересекают каналы (группы каналов), которые связывают её с другими подсистемами. Каждую такую группу будем называть пучком связей (аналогично определим пучок векторов). Все группы связей той или иной подсистемы образуют общую интегральную связь. Каждая общая интегральная связь обязательно содержит противоположно направленные векторы.
       Здесь у нас возникает необходимость уточнить понятие вектора. Дело в том, что при ближайшем рассмотрении появляется два разных типа векторов – вектор структуризации и вектор-связь.
       Что такое "вектор структуризации" рассмотрим на конкретном примере. В системе 1,1 можно выделить пять подсистем более низкого ранга: 2,1; 2,2; 2,3; 2,4; 2,5, каждая из которых тоже "дробится" на свои подсистемы, подуровни. Поэтому каждая из подсистем, на которые "распадается" 1,1, являет собой как бы направление дифференциации, вектор дифференциации, или, если рассматривать обратное направление – вектор структуризации. Вектор дифференциации (структуризации) включает в себя все связи, объединяющие элементы данной подсистемы (кроме тех, которые связывают основные подсистемы, они принадлежат вектору 1,1).
      Нечто иное представляет собой вектор-связь. Сущность его следующая. Любая пара элементов системы может быть связана между собой каналом взаимодействия. Его мы и называем собственно связью. Но, поскольку по каналу осуществляется движение потока ресурса – процесс направленный, то в этом контексте связь и можно определить как вектор-связь.
       В конечном счёте все связи системы соединяют элементы атомарного уровня (α-элементы), хоть для этого им приходится пересекать псевдограницы разных уровней разных подсистем. При этом количество пересечений псевдограниц разных подсистем одного и того же уровня (ранга) должно быть чётным!
       Теперь об обозначениях. В развитие изложенного выше примем для обозначения связи следующее выражение:

S=S(Z_i,E_i,G_i,L_i,R_i; Z_j,E_j,G_j,L_j,R_j)

      а для обозначения вектора такое:

V=V(Z_i,E_i,G_i,L_i,R_i; Z_j,E_j,G_j,L_j,R_j)

       Направление потока ресурса здесь примем от первой группы координат, заключённых в скобки, ко второй группе координат в тех же скобках. Пучок связей можно выразить как сумму составляющих его связей:

S_n=S(Z_i,E_i,G_i,L_i,R_i; Z_j,E_j,G_j,L_j,R_j)+ S(Z_k,E_k,G_k,L_k,R_k; Z_l,El,G_l,L_l,R_l)+…+ S(Z_m,E_m,G_m,L_m,R_m; Z_n,E_n,G_n,L_n,R_n)

       аналогично можно построить выражение для пучка векторов:

V_n=V(Z_i,E_i,G_i,L_i,R_i; Z_j,E_j,G_j,L_j,R_j)+ V(Z_k,E_k,G_k,L_k,R_k; Z_l,E_l,G_l,L_l,R_l)+…+ V(Z_m,E_m,G_m,L_m,R_m; Z_n,E_n,G_n,L_n,R_n)

       Но всего сказанного выше недостаточно для создания полного формального портрета системы. Дело здесь в том, что каждая система обладает набором свойств (тождественным набору функций), осуществляет какое-то изменение окружения посредством этих функций, каждая из которых характеризуется набором параметров. Поэтому для полноты формальной картины системы нам необходимо описать её как пространство изменений, пространство функцийи пространство свойств. Эти пространства позволят дополнить статический портрет системы – динамическим, их использование позволит показать систему как процесс.
       По сути, термины "свойство" и "функция" – синонимы. Свойство, по определению, есть "сторона предмета, обусловливающая его различие или сходство с другими предметами и проявляющаяся во взаимодействии с ними". Базовый набор свойств системы определяет её качество, уникальность. Но то или иное свойство системы может проявляться, а может не проявляться в зависимости от обстоятельств. Если свойства системы не проявляются, она бездействует, если проявляются – действует, функционирует. Таким образом, то или иное свойство системы проявляется через соответствующую её функцию, из чего мы можем сделать вывод, что функция – это активное свойство системы.
       Совокупность свойств-функций системы – это те изменения, которые она может осуществлять над потоком ресурса. Бывает, что преобразующих возможностей данной системы (подсистемы некой системы) недостаточно, тогда поток ресурса (или соответствующие его фрагменты) по каналам-связям отсылаются в другую систему (подсистему этой же системы) которая осуществляет необходимое дополнительное воздействие. Сумму таких воздействий можно назвать комплексным воздействием.
       Следовательно, взаимодействие между системами (точнее – содействие систем) может осуществляться только с помощью связи, а его содержание определяется изменениями характеристик потока ресурса. Отсюда видно, что сама связь также является важнейшей функцией системы – транспортной функцией. Таким образом, некий цикл функционирования системы заключается в том, что входной канал приносит и заводит в систему поток ресурса до изменения, а выходной – выводит и уносит поток ресурса после изменения. Сравнивая входной и выходной потоки, мы можем обнаружить изменения, которые произошли с ресурсом внутри системы (которая в этом случае играет роль "чёрного ящика". А уже на основе этих изменений можно определить, вычислить совокупность воздействий, функций, который данная система оказала на ресурс (а, в конечном счёте, структуру "чёрного ящика"). Раскрывая "чёрный ящик" (двигаясь внутрь структуры системы по её системному пространству), мы можем определить, какому из узлов (подсистем того или иного уровня) относится та или иная подгруппа функций. таким образом, мы можем добраться до атомарного уровня системы, до уровня тех её узлов, которые осуществляют элементарные воздействия (функции) на поток ресурса.
       Из сказанного можно сделать вывод, что существует некое взаимно-однозначное соответствие между структурным пространством системы в целом, структурой связей этой системы и пространствами её функций и свойств. Дальше мы попытаемся формализовать эти понятия.
       Определим как внешние те связи системы, которые пересекают её псевдограницу. Среди них будут как входные, так и выходные каналы. Функции (активные свойства, соответствующие этим связям), осуществляющие изменения потока ресурса на уровне псевдограницы системы, также назовём её внешними функциями. Хотя, если говорить строго, чисто внешних функций системы не существует, все воздействия системы на ресурс осуществляются внутри, в рамках её псевдограниц. Хоть конкретное изменяющее воздействие на ресурс осуществляется в узлах системы, любая связь, как мы уже договорились, несёт функциональный смысл, переносит результат воздействия узла, как бы проявляет какую-то функцию системы. А функцию, т. е. направленное действие, можно изобразить как некий вектор. Обозначим его символом f, тогда вектор --------->f есть некая функция системы Σ Таких функций может быть от 0 до n. В этом случае полный набор основных функций системы можно изобразить следующим образом:

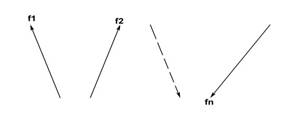
Рисунок 28

      Из этих векторов можно построить базис, определив его как пространство функций данной системы:

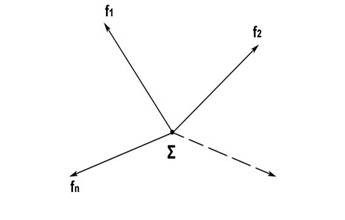
Рисунок 29

      Существует ли какое-то отличие между пространством свойств и пространством функций и если да, то в чём оно заключается? Это отличие действительно существует, и суть его такова, что свойство являет собой возможность, потенциал, а функция – реализацию, акт. Канал без потока ресурса – возможность, точно такой же возможностью является внешняя связь, если канал, скажем, блокирован. Собственно функция появляется лишь в процессе взаимодействия изменяемой и изменяющей сущностей.
      Договоримся изображать свойство системы также вектором, но единичным, тогда пространство свойств системы мы изобразим как единичный базис:

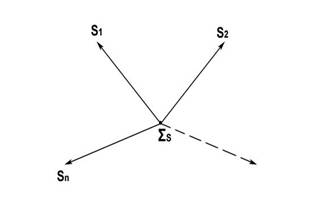
Рисунок 30

       где Σ_s означает систему свойств, а векторы S₁,S₂,…,S_n - отдельные свойства системы. Каждое свойство системы может проявляться с меньшей или большей интенсивностью, от нулевой (0), до максимальной (max) - [0,max]. Обозначим интенсивность символом η, тогда функцию системы в каждый момент времени можно определить как произведение её свойства на интенсивность: f_i=S_i * η_i, а пространство функций можно изобразить следующим образом:

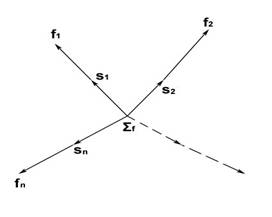
Рисунок 31

       Присвоим уровню организации системы, на котором проявляются её базисные функции, номер 1. Тогда на уровне с номером 0 будет проявляться интегральное свойство системы – её назначение (или роль) в гиперсистеме. Обозначим функцию,реализующую интегральное свойство системы Σ греческим символом Ρ (ро), что будет обозначать роль.

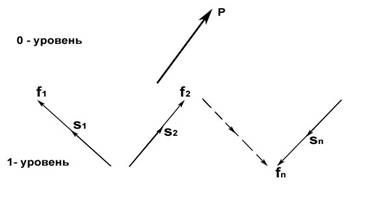
Рисунок 32

       Тогда вектор Ρ есть не что иное, как векторная сумма базисных функций системы:

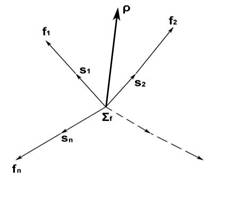
Рисунок 33

       При изменениях интенсивностей проявление свойств S₁, S₂, …, S_n системы Σ будет изменяться и её интегральная функция. Конец изображающего эту функцию вектора Ρ будет описывать при этом некоторую кривую в пространстве свойств-функций системы.
       Итак, Ρ есть интегральная функция системы Σ. Но каждый элемент этой системы тоже система, а, следовательно, обладает своим набором базовых функций и своей ролью в материнской системе. При этом между функциями соседних уровней существует следующая связь.
       Функции 1-го уровня порождают роль системы (функцию 0-уровня). Набор функций 2-го уровня порождает свои интегральные функции - ими как раз и являются функции 1-го уровня. То же самое по отношению к наборам функций 2-го уровня делают группы наборов функций 3-го уровня и т. д. вглубь системы, вплоть до уровня, определённого как атомарный. Наглядно изобразить эту зависимость можно следующим образом:

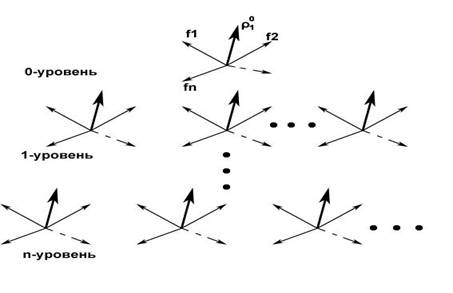
Рисунок 34

      Для описания пространства свойств-функций системы используем тот же формальный аппарат, что и для описания её структурного пространства. Основное отличие будет заключаться в замене главного объекта описания. В структурном пространстве это был узел, в пространстве свойств-функций это будет функция (и то, что с ней связано – свойство, связь, канал, вектор, поток ресурса).
      Вектор в структурном пространстве системы указывает направление диссоциации ("разукрупнения") узлов, а ещё являет интегральный образ связи, т. е. он как бы суммирует все связи – и входные, и выходные, которые коммутируют узел с его окружением.
       Возьмём ту же концентрическую диаграмму, которую мы использовали для изображения структурного пространства системы, но каждый из векторов диссоциации заменим на противоположный. В функциональном пространстве эти векторы мы обозначим как ρ-векторы – т. е. роли узлов в системе.

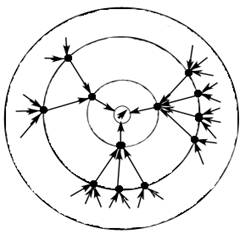
Рисунок 35

       Из этой схемы (а особенно из предыдущего рисунка, где изображена ролевая иерархия) видно, что группы ролевых векторов (интегральных функций) i+1-го уровня составляют базисы для ролевых векторов i-го уровня, а такие же группы векторов i-го уровня - базисы для интегральных функций i-1-го уровня. Возьмём координатную формулу для обозначения узла и запишем её для ρ-вектора:

Ρ=Ρ(Z,E,G,L,R);

       Здесь индексы выполняют то же самое назначение, что и в формуле для узла. Так, Z (зона, ранг) обозначает уровень организации системы, значения Z отсчитываются как и в структурном пространстве, т. е. от уровня системы как целого до её атомарного уровня. E означает номер интегральной функции на уровне i. G означает группу функций (базис) на уровне i или номер порождаемой этим базисом роли на уровне i-1. L и R означают левую и правую границу диапазона номеров группы функций (базиса) на уровне i+1, порождающего роль с номером E на уровне i.
       Но ролевой вектор, как и любой вектор, имеет начало и конец. В предыдущей формуле он описывался через координаты начала. Но любая интегральная функция связывает два уровня системы, а начало и конец вектора, изображающего эту функцию, описывается двумя наборами координат:

Ρ=Ρ(Z_i,E_i,G_i,L_i,R_i; Z_j,E_j,G_j,L_j,R_j)

       Интегральная функция - понятие относительное. Интегральной функцией мы называем всю совокупность воздействий, осуществляемых системой, т. е., её подсистемами внутри псевдограницы, связывая это суммарное воздействие с совокупностью активных каналов, пересекающих псевдограницу системы. Но конкретная связь-функция может пересечь не одну псевдограницу и связать элементы одного уровня разных подсистем.

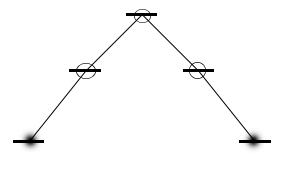
Рисунок 36

      Используем для её обозначения формулу:

F=F (Z_i,E_i,G_i,L_i,R_i; Z_j,E_j,G_j,L_j,R_j;K)

       где K - номер канала, пересекающего псевдограницу системы.
      Пожалуй, это всё, что нам нужно было сказать о системе ввиду поставленной задачи (формирования и обоснования необходимых элементов универсального языка). Мы ввели структурное и функциональное пространства для того, чтобы обнажить сущность преобразования (изменения), как такового и найти универсальный способ его описания. Только располагая таким способом, мы можем надеяться построить универсальный, строго формальный алгоритм описания самых разных систем.

г. Запорожье, 2009 г.

В начало книги

Предыдущая глава

Следующая глава

В конец книги